Pubblicato il 17 giugno 2018 su sportsbrain – Traduzione di Edoardo Salvati
// Quest’analisi prende spunto dall’articolo di David Robinson sulla stima empirica di Bayes, un metodo statistico utilizzato per stimare un grande numero di percentuali. Qui l’idea è di prevedere il numero di ace sulla base del numero di game al servizio giocati in una determinata partita.
Entrando nel dettaglio, si definisce la frequenza di ace di un giocatore come il numero di ace diviso per il numero di game al servizio in una partita. Per la stima della frequenza di ace, si può usare uno stimatore empirico di Bayes mediante una distribuzione Beta. Per chiarezza, la distribuzione Beta è una famiglia delle distribuzioni di probabilità continua definita da due parametri positivi alfa e beta nell’intervallo unitario [0,1].
Definizione dello stimatore e dei parametri
Il primo passo in una stima empirica di Bayes è la definizione dello stimatore Beta a priori rispetto ai dati delle partite a disposizione (dall’inizio della stagione 2016 fino al 28 maggio 2018). L’immagine 1 mostra la densità della frequenza di ace dei vincitori in partite terminate in tre set.
IMMAGINE 1 – Distribuzione della frequenza di ace dei vincitori in partite di tre set.
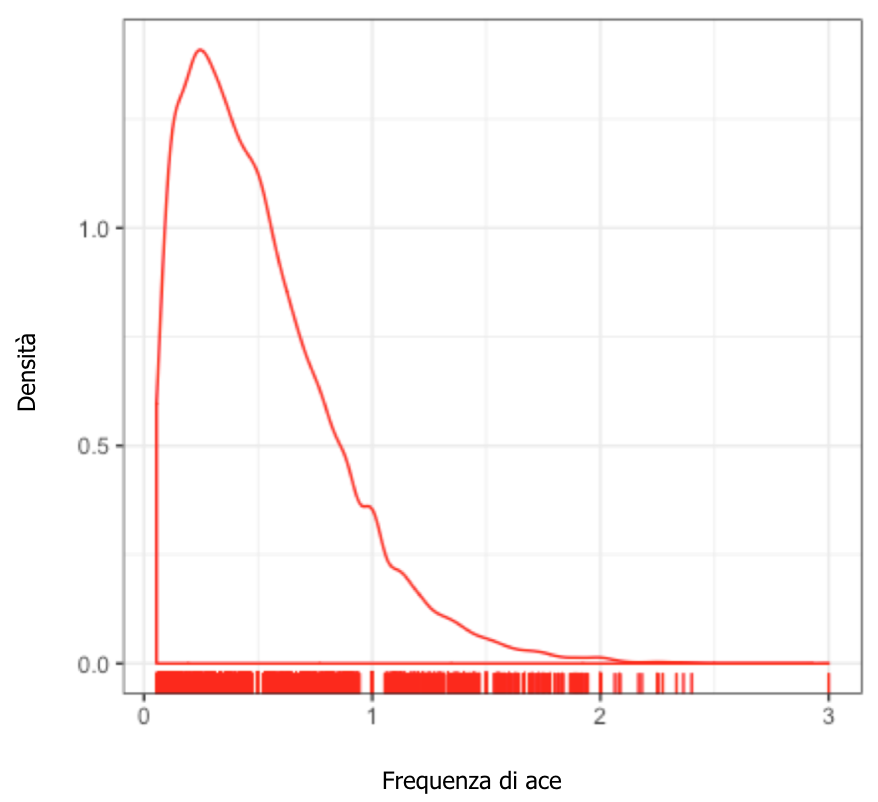
Serve anche selezionare gli “iper-parametri” alfa e beta per il modello Beta che, in questo caso, hanno un valore rispettivamente di 1.76 e 10.83. Si può poi aggiornare la distribuzione Beta con i dati delle singole partite, vale a dire la frequenza degli ace per ciascun giocatore.
Applichiamo ora i parametri alfa e beta per provare a stimare la frequenza di ace nel caso un giocatore avesse servito cinque ace in dodici game al servizio. La modifica ai parametri alfa e beta cambia il modo in cui il modello si adatta ai dati a disposizione. Noti i valori di alfa e beta e la distribuzione Beta possiamo ottenere una stima della frequenza di ace di un giocatore come segue:
5 + alfa / 12 + alfa + beta = (5+1.76/12+1.76+10.83) = 0.274
Vale a dire, la stima della frequenza di ace per questo giocatore sarebbe del 27.4%. Il grafico di immagine 2 suggerisce che il modello Beta creato ha stimato con accuratezza la frequenza di ace sulla base dei dati dalle partite.
IMMAGINE 2 – Stima della frequenza di ace (asse delle X) di ciascun giocatore rispetto alla frequenza effettiva (asse delle Y)
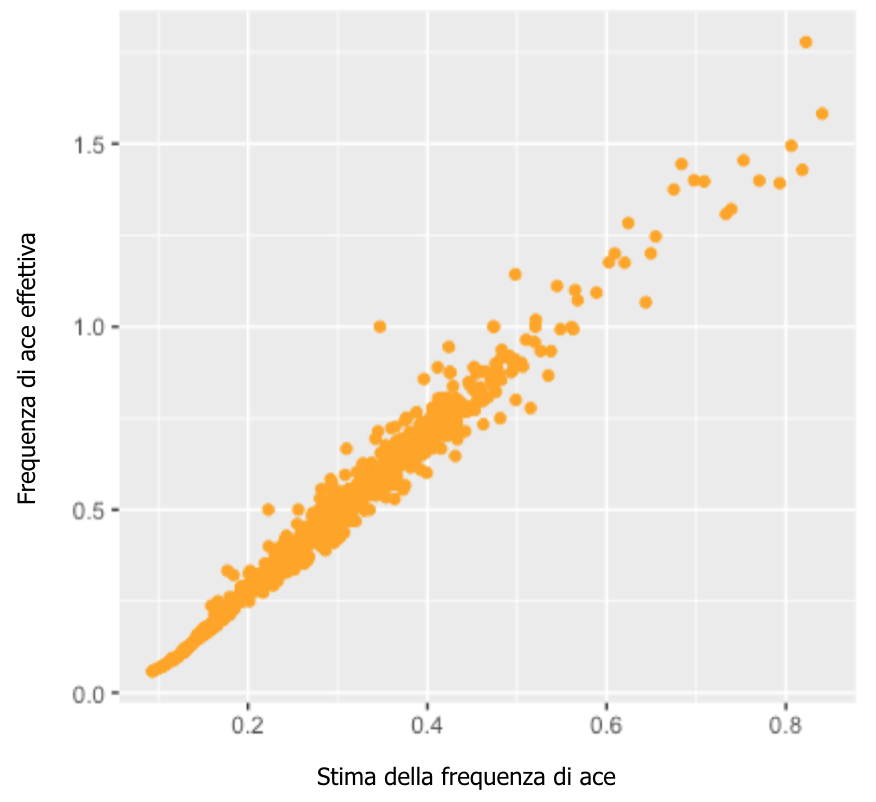
Più ace non portano per forza a una classifica di vertice
La tabella elenca le prime 20 stime di frequenza di ace e la relativa frequenza effettiva usando la distribuzione Beta a priori per la stima della frequenza di ace della singola partita.
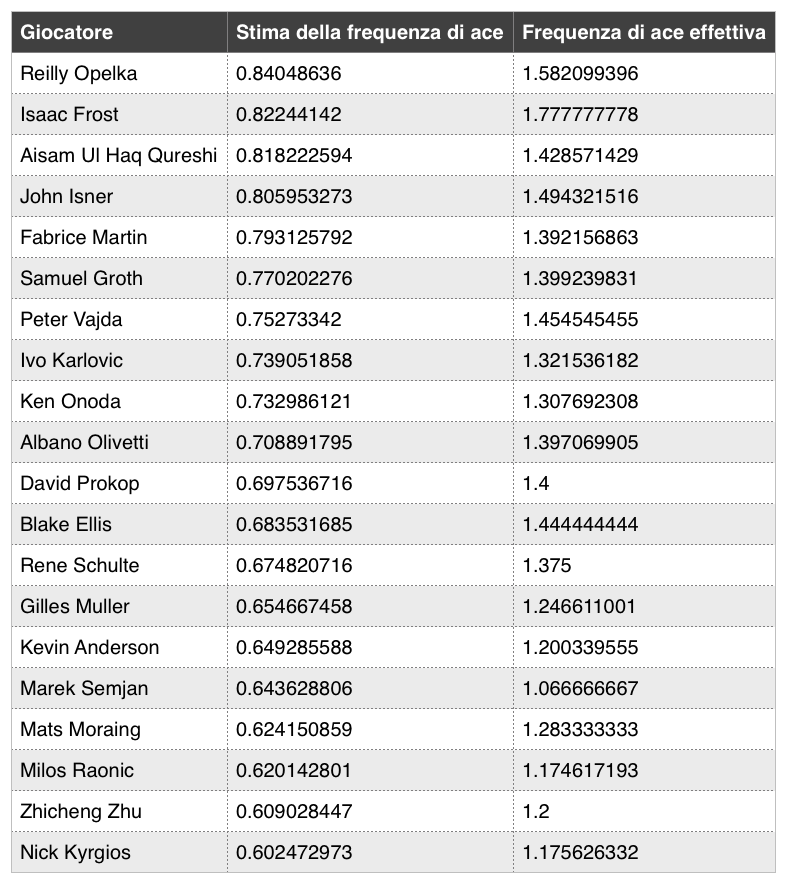
Troviamo una combinazione di giocatori noti e meno noti. Non sorprende la presenza di John Isner (1.49 di frequenza ace effettiva) e Ivo Karlovic (0.74 di frequenza stimata) tra i più alti valori stimati dal modello, considerando la loro efficacia al servizio.
Questi nomi però dimostrano che un’alta frequenza di ace non necessariamente si traduce in una classifica di vertice. Rafael Nadal e Roger Federer non collezionano ace a profusione, ma si può dire che siano stati probabilmente i due giocatori di massimo vertice negli ultimi dieci anni.
Complessivamente, il modello Bayesiano tende a una leggera sottostima della frequenza effettiva di ace di ciascun giocatore, ma è un buon metodo di stima, a cui sarà utile rivolgersi nella previsione di altre statistiche di tennis in futuro.
Il codice dell’analisi è disponibile qui. ◼︎
Elite Tennis Players Don’t Always Have the Highest Ace Rates


