di Chapel Heel // HiddenGameOfTennis
// Negli ultimi giorni, i tifosi di Rafael Nadal si sono lamentati a gran voce su Twitter perché Wimbledon ha disonorato la classifica ufficiale assegnando a Nadal la testa di serie numero 3, invece della 2. Non mi è chiaro se non siano a conoscenza della formula usata per determinare le teste di serie, se non sia di loro gradimento, o se ritengono che non ci dovrebbe essere alcuna formula diversa dagli altri tornei. Detto questo, e considerando che Nadal può incidere sul processo (ad esempio giocando e vincendo di più sull’erba), quali sono le conseguenze legate a un declassamento dalla seconda alla terza testa di serie in uno Slam?
Si può pensare che ce ne siano se la testa di serie numero 1 è davvero una minaccia per la vittoria finale del torneo, come evidentemente nel caso di Novak Djokovic a Wimbledon. La numero 2 può giocare contro la numero 1 solo in finale, mentre la numero 3 ha il 50% di probabilità di capitare nello stesso lato di tabellone e quindi doverla affrontare nell’eventuale semifinale, aspetto che dovrebbe diminuire le probabilità di raggiungere la finale.
Wimbledon 2019
Ora che il tabellone di Wimbledon è definito, si può misurare l’importanza di avere la testa di serie numero 2 anziché la numero 3.
Tabellone effettivo
La tabella mostra le prime otto teste di serie a Wimbledon (in ordine di piazzamento nel tabellone). Il primo gruppo di colonne riporta le mie previsioni Elo preliminari rispetto alla situazione effettiva. Il secondo gruppo è una simulazione a teste di serie invertite (Nadal con la numero 2 e Federer con la 3), pur lasciando inalterato l’elenco dei nomi in modo da avere un confronto più immediato. Le ultime due colonne evidenziano il cambiamento in termini di probabilità per la finale e la vittoria se si scambia Nadal con Federer. Numeri positivi (su sfondo verde) indicano un miglioramento con Nadal testa di serie numero 2, e così via.
IMMAGINE 1 – Previsioni Elo per le prime 8 teste di serie a Wimbledon, con tabellone effettivo e inversione delle teste di serie 2 e 3
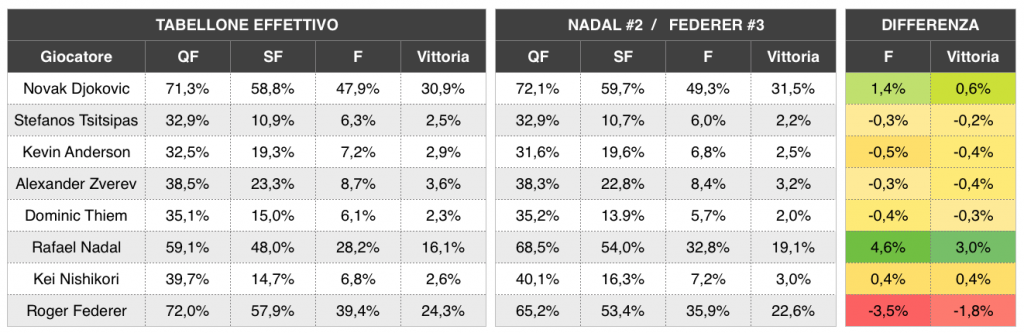
Come ci poteva attendere, lo scambio incide più sulla probabilità di arrivare in finale che di vincere il torneo. Differenze in valore di 0.5% sono solo variazioni casuali nella simulazione, mentre hanno rilevanza quelle tra Nadal e Federer (oltre a una leggera diminuzione della probabilità di Djokovic nel caso Nadal fosse stato la numero 2).
Riseminare il tabellone
Eseguiamo una nuova simulazione, questa volta però con 100.000 configurazioni del tabellone principale. Nel primo insieme, Federer è la testa di serie numero 2 e Nadal la 3, nel secondo insieme le posizioni sono invertite. Come sopra, l’ordine dei nomi rimane identico.
IMMAGINE 2 – Previsioni Elo per le prime 8 teste di serie a Wimbledon, con simulazione e inversione delle teste di serie 2 e 3
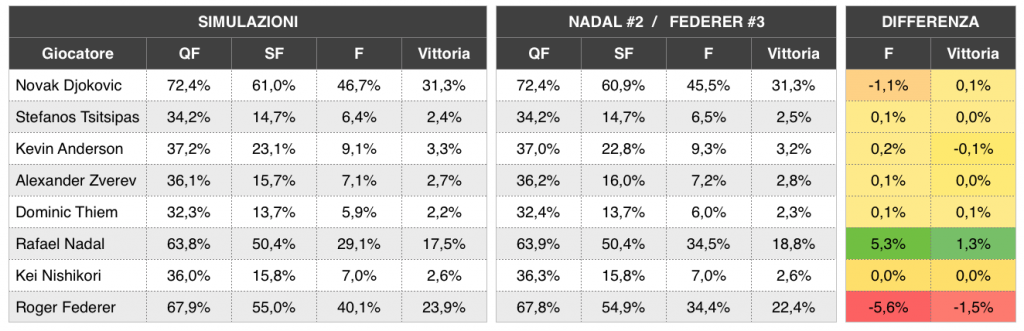
Mi aspettavo che l’effetto delle 100.000 configurazioni appiattisse la differenza riscontrata nella tabella precedente, e così è stato relativamente alla vittoria del torneo. A essere più marcata è ora la variazione di percentuale nella probabilità di raggiungere la finale.
Niente di questo dovrebbe però diventare motivo di legittimazione per i tifosi di Nadal alla lamentela sull’assegnazione delle teste di serie. Solo perché la differenza di posizione nel tabellone effettivo ha rilevanza, non significa che Nadal abbia ricevuto la testa di serie sbagliata.
La testa di serie numero 2 e numero 3 a confronto negli altri Slam del 2019
Si potrebbe replicare la stessa analisi per qualsiasi torneo passato, anche non Slam. Visto che Nadal era testa di serie numero 2 sia agli Australian Open che al Roland Garros (vi chiederete, perché non la numero 1?) mentre Federer la numero 3, ho considerato solo quei due Slam per un ulteriore esame delle conseguenze di scambio tra teste di serie. Aiuta anche il fatto che Djokovic era la numero 1 in entrambi i tornei.
Nelle tabelle che seguono, ho sostituito i nomi dei giocatori con i numeri delle teste di serie, perché le restanti cinque delle prime otto teste di serie non erano identiche, come nel caso di Wimbledon.
Roland Garros 2019
Diversamente da Wimbledon e dagli Australian Open, il dominio di questo torneo da parte di Nadal rende la simulazione più complicata, perché la previsione di una sua vittoria, ogni anno, è scandalosamente alta. Di conseguenza, ci si può attendere che spostarne la posizione
nel tabellone (in questo caso dalla numero 2 alla numero 3) avrà un impatto sostanziale, forse su tutti i giocatori con una almeno discreta probabilità di vittoria.
IMMAGINE 3 – Inversione delle teste di serie 2 e 3 al Roland Garros 2019
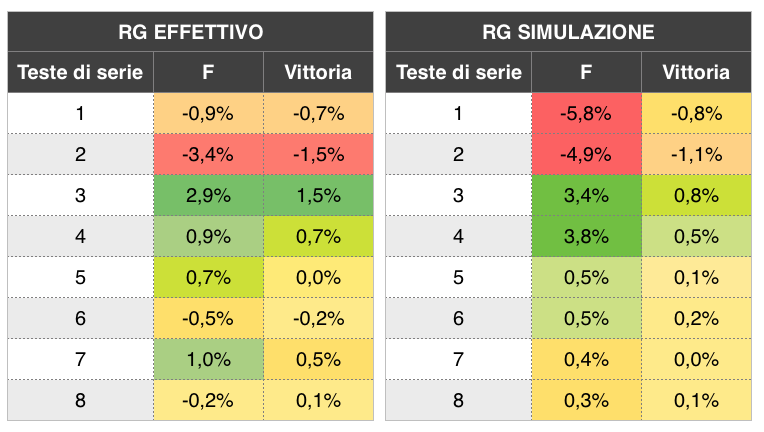
La conseguenza di una redistribuzione delle teste di serie numero 2 e 3 al Roland Garros 2019 è all’incirca la stessa di Wimbledon sia nello scenario del tabellone effettivo, sia nelle 100.000 simulazioni. Rispetto a Wimbledon però, c’è un effetto sulle altre teste di serie, specialmente su Djokovic quando si effettua la riconfigurazione. Parte è attribuibile al fatto che Nadal entra nel lato di Djokovic prima della finale, parte dalla facilità, o non facilità, del tabellone effettivo avuto al Roland Garros. Inoltre, come testa di serie numero 4 Dominic Thiem ha avuto un impatto maggiore sull’esito del torneo di quanto ci si possa aspettare da Kevin Anderson a Wimbledon, sempre da numero 4.
Australian Open 2019
Dato un maggiore equilibrio, o che tale avrebbe dovuto essere, tra le probabilità dei primi 3 agli Australian Open, mi sarei aspettato dei risultati più simili a Wimbledon che al Roland Garros, vale a dire che la numero 2 e 3 subiscono un effetto rilevante, forse la numero 1 qualcosa, ma nessuna delle altre. Inoltre la simulazione fatta alla vigilia degli Australian Open suggeriva che non c’era molta differenza tra il tabellone effettivo e le altre configurazioni, quindi per questo torneo la fortuna del sorteggio non dovrebbe contare.
IMMAGINE 4 – Inversione delle teste di serie 2 e 3 agli Australian Open 2019
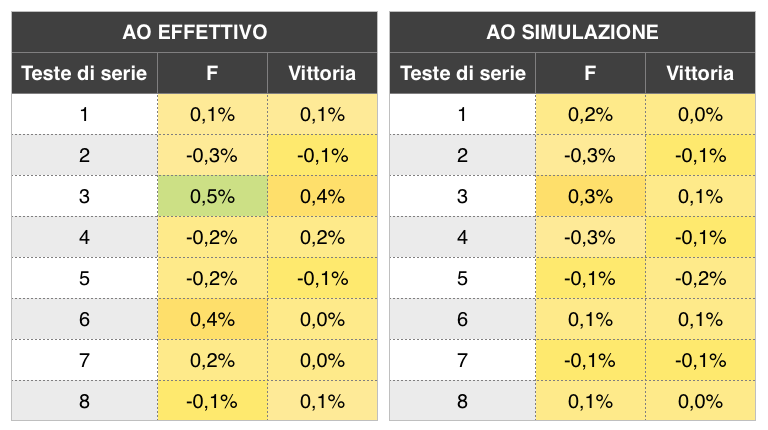
Beh, non pensavo proprio che andasse così, praticamente nessuna conseguenza di uno scambio tra Nadal numero 2 e Federer numero 3, sia nello scenario del tabellone effettivo che in quello delle 100.000 riconfigurazioni. Un tabellone equilibrato e le probabilità relative dei primi 8 sul cemento sembrano aver controbilanciato, fino ad annullare, la possibile incidenza dell’inversione tra la numero 2 e la numero 3.
Risolvere per x
Anche se a Wimbledon e al Roland Garros quest’anno lo scambio di teste di serie tra Nadal e Federer avrebbe avuto delle conseguenze, non c’è stata di fatto alcuna differenza agli Australian Open.
Questo mi fa pensare che nella pratica l’effetto dovuto al cambiamento tra numero 2 e numero 3 è altamente dipendente da tre fattori e dalla loro combinazione: a) il successo atteso dei giocatori di vertice su una determinata superficie (più estremo sull’erba e sulla terra, meno sul cemento), e/o b) il relativo bilanciamento, in termini di talento, tra le prospettiche teste di serie 2 e 3, che al momento sono due dei giocatori più grandi di sempre in grado di vincere su qualsiasi superficie in qualsiasi occasione, e/o c) la casualità del tabellone effettivo.
Sarebbe interessante applicare lo stesso metodo per gli Slam degli scorsi anni, così da verificare il livello di incidenza della superficie o del tabellone specifico sugli effetti dello scambio tra teste di serie 2 e 3. È sempre pronunciato a Wimbledon e al Roland Garros, ma meno importante agli Australian Open? O dipende dai giocatori che in quel momento occupano le posizioni dalla testa di serie numero 4 alla numero 8? Quanto influisce se il tabellone effettivo è rappresentativo della media di molti tabelloni alternativi rispetto a essere un tabellone fortunato o sfortunato per i giocatori di vertice? Si dovrebbe tenere conto di molti fattori e si dovrebbero includere moltissimi tornei per ottenere risultati affidabili.
Per adesso, sulla base dei tabelloni e delle previsioni per gli Slam 2019, dobbiamo trovare un punto di convergenza per un intervallo di x approssimativamente tra 0% e -5%. ◼︎


