Pubblicato il 14 novembre 2019 su betfair | The Hub – Traduzione di Edoardo Salvati
// Ho scritto in precedenza del sistema di valutazioni Elo, che è risultato il modello più efficace tra quelli pubblicamente disponibili per fare previsioni sulle partite di tennis. In questo articolo approfondisco un’altra classe di modelli, quelli basati sulle situazioni di punteggio. Pur non avendo lo stesso potere di Elo nell’individuare il risultato finale, permettono di pronosticare un numero molto più ampio di singoli elementi di una partita, come il numero di set, il numero di game e perfino il numero di punti.
L’ipotesi di probabilità indipendente e identicamente distribuita
Come si evince anche dal nome, i modelli basati su situazioni di punteggio creano relazioni matematiche per prevedere l’esito di una partita di tennis partendo dal singolo punto. Tipicamente, l’ipotesi di fondo che li guida è che la probabilità di vincere un punto al servizio in una partita è indipendente e identicamente distribuita (i.i.d.). Per quanto riguarda l’indipendenza, questo significa che la probabilità di vincere un punto al servizio non è influenzata dal risultato dei punti precedenti. In altre parole, è annullato il concetto di vantaggio psicologico: la probabilità rimane costante, a prescindere dal fatto che il giocatore abbia vinto (o perso) gli ultimi punti giocati. La caratteristica della probabilità di essere identicamente distribuita significa invece che ogni punto è considerato allo stesso modo: la probabilità di vincerlo rimane la medesima a prescindere che si tratti di un punto delicato nel set decisivo o di un punto di poco peso nel primo set.
Sono attributi che si scontrano con l’intuizione legata al vantaggio psicologico e alla pressione. Ma è davvero così? Franc Klaassen e Jan Magnus sono in realtà arrivati a conclusioni di altro tipo: è più probabile infatti che i giocatori vincano un punto al servizio se hanno vinto il precedente (a suggerire l’esistenza di un vantaggio psicologico) ed è meno probabile che vincano il punto se si tratta di uno molto importante (a suggerire l’esistenza della pressione). Hanno trovato però che questi effetti sono abbastanza deboli e che l’ipotesi di probabilità indipendente e identicamente distribuita è valida ai fini delle previsioni nel tennis. Come vedremo più avanti, è proprio questa la forza dell’ipotesi, cioè consentire di fare previsioni dettagliate sulla partita, non solo sul vincitore ma anche sul margine di vittoria.
Utilizzare l’ipotesi i.i.d.
Per comprendere come l’ipotesi i.i.d. aiuti nella costruzione del modello, consideriamo un game al servizio. L’ipotesi i.i.d. richiede di porsi nell’ottica di una partita di tennis come una sequenza di lanci di moneta truccati: ogni volta che un giocatore è al servizio, vince o perde il punto secondo una probabilità fissa pS, a prescindere dal momento in cui si trova la partita. Vincere il game di servizio a zero equivale a quattro “lanci di moneta” di fila, cioè pS^4. Considerando tutti i possibili modi in cui si può vincere un game al servizio (passando anche per le parità) e aggiungendo la variabile tempo, gli autori Paul Newton e Joseph Keller sono arrivati a un’equazione per la probabilità di vincere un game al servizio come rappresentata nell’immagine 1.
IMMAGINE 1 – Equazione della probabilità di vincere un game al servizio
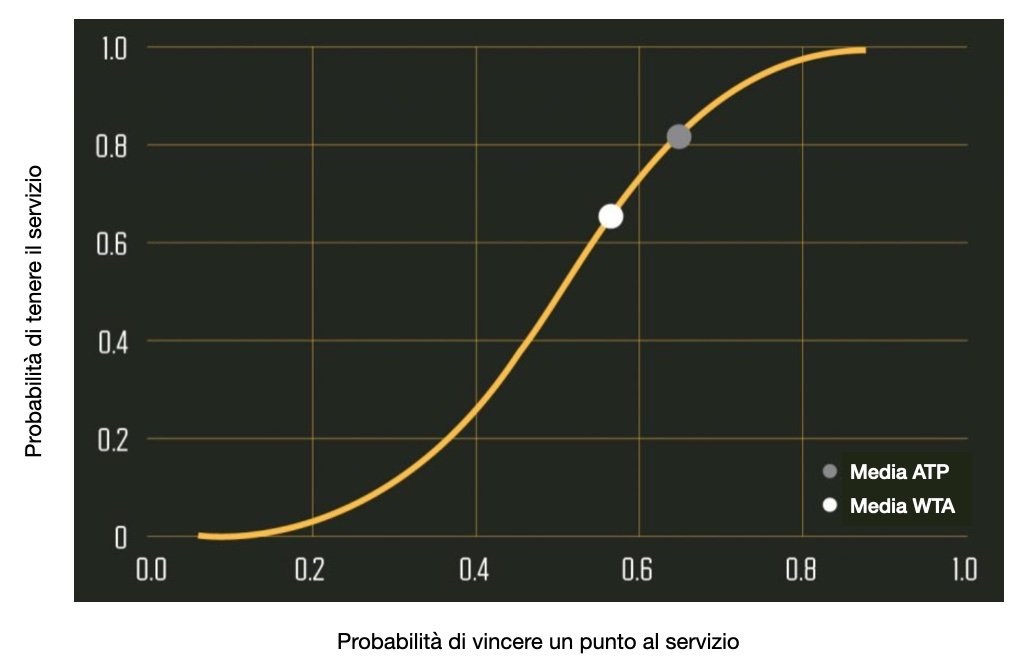
Si osserva una forma semplice generata dalla probabilità. È anche interessante notare che in corrispondenza della media del 56% di punti vinti al servizio nel circuito maggiore femminile, la probabilità di tenere il servizio è del 65%, contro una media del 64% per gli uomini e una probabilità dell’81%. Una differenza così ampia spiega come mai break al servizio sono molto più comuni nelle partite WTA che in quelle ATP.
Fare previsioni sulle partite con l’ipotesi i.i.d.
Newton & Keller hanno calcolato anche la probabilità di vincere un set, un tiebreak, la partita, oltre alla probabilità di specifiche situazioni di punteggio, usando solo la probabilità di vincere un punto al servizio per ciascuno dei due giocatori. Sono passaggi un po’ complicati da illustrare in un contesto di più generico come questo. Voglio invece mostrare come i fattori di un modello i.i.d. possono essere derivati utilizzando un particolare modello di questa classe, e poi fare alcuni esempi delle previsioni che si riescono a generare. Tutti i dati necessari per sviluppare le equazioni i.i.d. sono contenute nel lavoro di Newton & Keller.
Il modello Barnett & Clarke
Nell’analisi eseguita da Stephanie Kovalchik sui modelli basati sulle situazioni di punteggio, il migliore è stato quello pubblicato nel 2005 da Tristan Barnett e Stephen Clarke della Swinburne University. La formula con cui viene calcolata la probabilità di un giocatore i di vincere il punto al servizio contro il giocatore j è la seguente:
fij= ft + [fi– fav] – [gj – gav].
Possiamo suddividere questa equazione in tre termini.
ft :
Si riferisce alla probabilità media per il torneo di vincere un punto al servizio. È un termine importante perché alcuni tornei hanno superfici “veloci” e, in media, aiutano il giocatore al servizio, come Wimbledon. Altri, come il Roland Garros, sono “lenti”, con effetto opposto. Nel 2014 ad esempio, la probabilità media di vincere un punto al servizio era del 67.2% a Wimbledon contro il 62.4% al Roland Garros.
[fi– fav] : fi
fi è la probabilità media del giocatore i di vincere un punto al servizio, e fav è la media del circuito al servizio. Questo termine ha un valore maggiore di zero se il giocatore i è più forte al servizio del giocatore medio del circuito, negativo se invece il giocatore ha una resa al servizio inferiore alla media.
[gj – gav] : gj
gj è la probabilità media del giocatore j di vincere un punto alla risposta, e gav è la media del circuito alla risposta. Come per il termine precedente, anche questo è positivo se il giocatore j è più forte alla risposta del giocatore medio del circuito, negativo nel caso opposto.
Il modello funziona in questo modo: si prende la media di punti vinti al servizio nel torneo e la si aumenta in relazione a quanto il giocatore è più forte al servizio della media del circuito e la si diminuisce di quanto l’avversario è più forte alla risposta della media del circuito. Così facendo, si tiene conto sia della abilità al servizio del giocatore i che della bravura alla risposta del giocatore j, oltre alla velocità di superficie del torneo.
Un esempio concreto dalla finale di Wimbledon 2015
Per vedere come funziona in concreto il modello di Barnett & Clarke, consideriamo le previsioni associate a una partita specifica, come la finale di Wimbledon 2015 tra Novak Djokovic e Roger Federer. La tabella riepiloga la probabilità media di vincere un punto al servizio e alla risposta per entrambi nelle 52 settimane precedenti.
Giocatore fi gi Djokovic 70.4% 44.6% Federer 72.3% 41.1%
Prima della finale, Federer aveva una percentuale più alta di punti vinti al servizio, mentre Djokovic era più forte alla risposta. Per arrivare alla stima di Barnett & Clarke, abbiamo bisogno anche delle medie del circuito, riepilogate dalla tabella.
Media fav 64% gav 36% ft 67.2%
Inserendo le informazioni nell’equazione di Barnett & Clarke, otteniamo una previsione di probabilità di vincere il servizio del 67.0% per Federer e del 68.6% per Djokovic.
Applicare il modello i.i.d. con queste stime
Con le equazioni di Newton & Keller, possiamo calcolare la probabilità che Djokovic o Federer avevano di vincere la partita. Considerando che era al meglio dei cinque set e con le probabilità al servizio appena calcolate, Djokovic aveva una probabilità di vittoria del 59.4% e Federer una del 40.6%. Il modello i.i.d. permette di scomporre questa probabilità anche sul numero di set.
IMMAGINE 2 – Probabilità sul numero di set per la finale di Wimbledon 2015
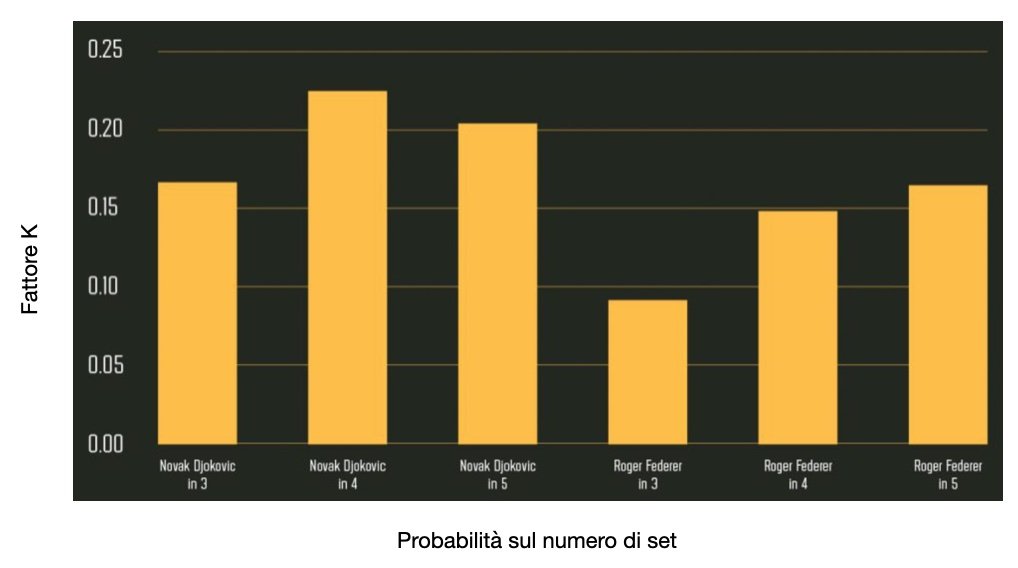
Si nota come la vittoria di Djokovic in 4 set era la previsione più probabile, seguita dalla sua vittoria in 5 set. La partita è terminata con il punteggio di 7-6(1) 6-7(10) 6-4 6-3 per Djokovic quindi, in questo caso, il modello si è comportato egregiamente.
Guardiamo ora anche ai punteggi più probabili. L’equazione di Newton & Keller permette di calcolare la probabilità pS (i,j), cioè la probabilità di arrivare a qualsiasi punteggio i,j in un set. L’immagine 3 mostra il risultato della stima di Barnett & Clarke per la finale di Wimbledon 2015.
IMMAGINE 3 – Punteggio più probabile per ogni set se visto per Djokovic
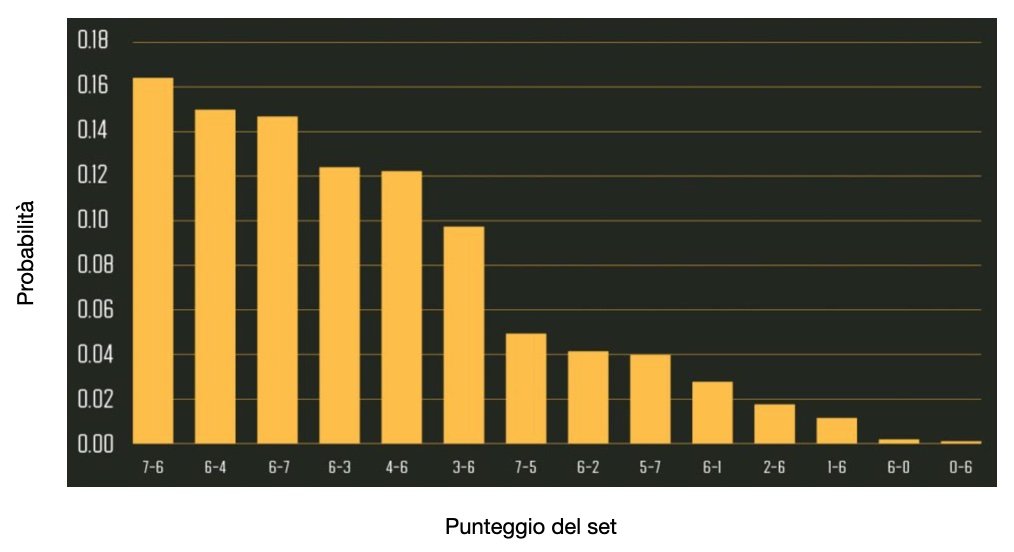
I punteggi che il modello i.i.d. giudicava come più probabili sono anche quelli che si sono poi concretamente verificati. Un’ultima interessante proprietà del modello è di poter calcolare probabilità di vittoria aggiornate in ogni momento della partita. Il grafico dell’immagine 4 mostra la variazione della probabilità di vittoria per Djokovic nello sviluppo della partita.
IMMAGINE 4 – Variazione della probabilità di vittoria di Djokovic nello sviluppo della partita
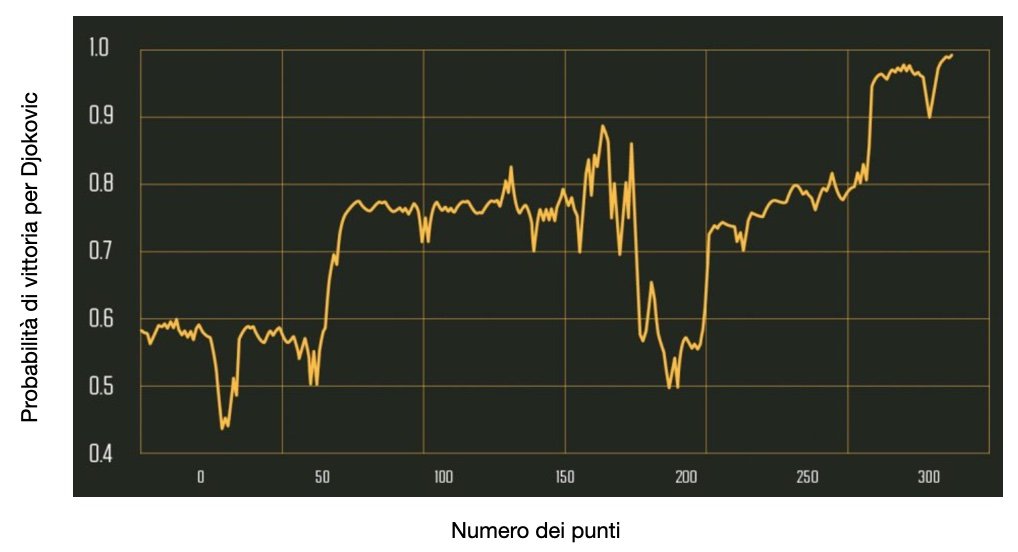
Come detto, all’avvio della partita Djokovic aveva una probabilità di vittoria del 59.4%, che rimane stabile prima di calare bruscamente al 45% intorno al trentesimo punto, cioè quando Federer fa il break e sale sul 4-2. Djokovic però fa un immediato contro-break, portando di fatto la partita in parità (probabilità sul 50%). Il cambiamento sostanziale successivo arriva dopo che Djokovic vince il primo set. Con un punteggio di 7-1 nel tiebreak, intorno al punto 70 la curva aumenta verticalmente fino quasi a raggiungere il 75%. Un lungo secondo set si conclude con Federer che chiude un tiebreak epico per 12-10, portando il punteggio sull’1-1 e la probabilità di Djokovic al livello iniziale. Nel terzo set però Djokovic sale sul 3-1, e la sua probabilità torna al di sopra del 70%. Vincendo il terzo set e dopo il break sul servizio di Federer nel quarto, la vittoria è praticamente assicurata.
Riepilogo
I modelli basati sulle situazioni di punteggio sono composti da elementi: da un lato, un modello di partita di tennis basta sulla probabilità di vincere un punto al servizio (che si assume costante, o indipendente e identicamente distribuita per la durata della partita), dall’altro un modello per fare previsioni di queste probabilità.
Il migliore tra i modelli di questa famiglia — quello di Barnett & Clarke corretto per avversario — non ha la stessa resa predittiva del sistema di valutazioni Elo, ma offre una pletora di previsioni aggiuntive. I modelli basati sulle situazioni di punteggio non necessariamente fanno peggio di Elo: è anzi possibile trovare probabilità di vincere il servizio in linea con quanto espresso da Elo o da altri modelli.
Un limite dei modelli i.i.d è che, come premesso all’inizio, l’ipotesi di fondo è vera solo come approssimazione. Molti lavori, tra cui uno di cui sono co-autore, hanno analizzato il comportamento dei giocatori rispetto all’ipotesi di probabilità costante. Anche se in generale le variazioni sono minime, tenerne conto potrebbe migliorare le stime, in particolare per quelle nel corso della partita.
Complessivamente, questi modelli predittivi sono tra i più efficaci, e fanno la differenza per il numero di informazioni che riescono a produrre sulla partita. Come nel caso della finale di Wimbledon 2015, le previsioni arrivano a essere incredibilmente precise, nel punteggio e nel numero di set. Naturalmente, non sempre il risultato è perfetto ma, per quanto inferiori a Elo, sono comunque modelli competitivi e di grande interesse. ◼︎


